The figure above illustrates the method:(a) Goal-conditioned RL often fails to reach distant goals, but can successfully reach the goal if starting nearby (inside the green region). (b) Our goal is to use observations in our replay buffer (yellow squares) as waypoints leading to the goal. (c) We automatically find these waypoints by using the agent’s value function to predict when two states are nearby, and building the corresponding graph. (d) We run graph search to find the sequence of waypoints (blue arrows), and then use our goal-conditioned policy to reach each waypoint.
tldr: Search on the Replay Buffer is a simple trick for improving a goal-conditioned RL agent without retraining.
Reinforcement learning (RL) has seen a lot of progress over the past few years, tackling increasingly complex tasks. Much of this progress has been enabled by combining existing RL algorithms with powerful function approximators (i.e., neural networks). Function approximators have enabled researchers to apply RL to tasks with high-dimensional inputs without hand-crafting representations, distance metrics, or low-level controllers. However, function approximators have not come for free, and their cost is reflected in notoriously challenging optimization: deep RL algorithms are famously unstable and sensitive to hyperparameters.
RL is not the only method to teach machines to take smart actions: planning-based approaches can solve many of the same problems. Planning-based approaches typically build a graph to represent the environment and then choose actions by computing a shortest path in this graph. Planning algorithms, such as A* and probabilistic roadmaps (PRMs), work amazingly well on some tasks (Kalisiak 2001, Lau 2005, Park 2016). However, planning algorithms are limited to tasks where it is easy to (1) generate or sample valid states, (2) determine the distance between pairs of states and (3) design a local policy for reaching nearby states, requirements that become roadblocks when applying these planning algorithms to tasks with high-dimensional observations (e.g., images). How can we combine the scalability of deep RL with the stability and robustness of planning algorithms?
Our recent NeurIPS paper, Search on the Replay Buffer, is a step in this direction: the method we propose merges deep RL with planning, using the strengths of each to overcome the shortcomings of the other. The method can be interpreted in two lights:
- Making RL easier via planning: We use planning algorithms to automatically decompose long-horizon control tasks into a sequence of easier problems, each of which is significantly easier for deep RL to solve, as compared to the original problem.
- Making planning easier via RL: We use deep RL to automatically learn distance metrics and local policies, removing two major barriers to using planning algorithms.
Search on the Replay Buffer
In the rest of this post, we describe one method to combine planning and reinforcement learning. We should emphasize that we are not the first to consider combining planning and RL (Faust 2017, Savinov 2018, Zhang 2018, Akkaya 2019). We will be interested in learning a goal-conditioned policy, which takes as input the current state \(s\) and the goal state \(s_g\) and outputs actions to navigate to the goal. The main building block of our method is goal-conditioned RL (see, e.g., [Kaelbling 1993]), which uses RL to learn such a goal-conditioned policy. In goal-conditioned RL the reward function \(r(s, a, s_g)\) depends on the current state and action as well as the goal state. Empirically, existing goal-conditioned RL algorithms, which use a process of trial and error to maximize this reward function, can learn to reach nearby goal states (i.e., when \(s\) is close to \(s_g\)) but fail to reach far away goal states. Our method, which combines existing goal-conditioned RL algorithms with planning algorithms, will be much more adept at reaching distant goal states.
As mentioned in the introduction, planning algorithms require three ingredients: (1) a set of valid states from which to sample; (2) a local policy for navigating between nearby states; and (3) estimates for the distances between all pairs of states. One of our key ideas is using existing goal-conditioned RL algorithms to procure these ingredients:
- Sampling States: This is the easiest ingredient to procure. We will save every observation that we have seen. The data structure that stores this experience is known as a replay buffer. This replay buffer is a standard part of RL algorithms, and will be filled when we learn the goal-conditioned policy (in the next step). To sample states, we will choose an observation uniformly at random from this replay buffer. Note that these states may be high-dimensional (e.g., images).
- Goal-Conditioned Policy: We will use the policy acquired by goal-conditioned RL. While it is often quite challenging to use RL to learn policies for solving long horizon tasks, we will only need our goal-conditioned policy to be able to reach nearby states.
- Estimating Distances: We can estimate the distance between states using the output of a carefully-constructed Q-function. For the task of reaching goal state \(s_g\), an agent at state \(s\) that takes action \(a\) receives a reward \(r(s, a, s_g) = -1\). Since the episode terminates when the agent reaches the goal, the cumulative reward corresponds to the negative number of steps to reach that goal state. Thus, we can use the (negative) predicted Q-values are our estimate for the distance between states: \(d(s, a, s_g) = -Q(s, a, s_g)\). We should note that getting accurate distances required a few tricks, including ensembles and distributional RL, that we describe in more detail in the paper.
Having acquiring these three ingredients, we will use them to navigate from any state to any other goal state. The first step is to automatically find a coarse set of waypoints leading to the goal. We do this by constructing a complete graph, where nodes are states (e.g., images) sampled from the replay buffer and each edge length corresponds to the predicted distance between those nodes. We use Dijkstra’s Algorithm to find the shortest path on the graph from the start state to the goal state (if the start state or goal state weren’t in the graph to begin, we’d add them). The shortest path consists of a sequence of waypoints leading to the goal, though each waypoint may be many steps apart. The second step is to use our goal-conditioned policy to reach each of the waypoints, in turn. Because the waypoints are spaced much closer together than the final goal, it is easier for the policy to reach each. We call this algorithm Search on Replay Buffer (SoRB), and provide a simple illustration of the algorithm in the figure at the top of this post.
Experimental Results
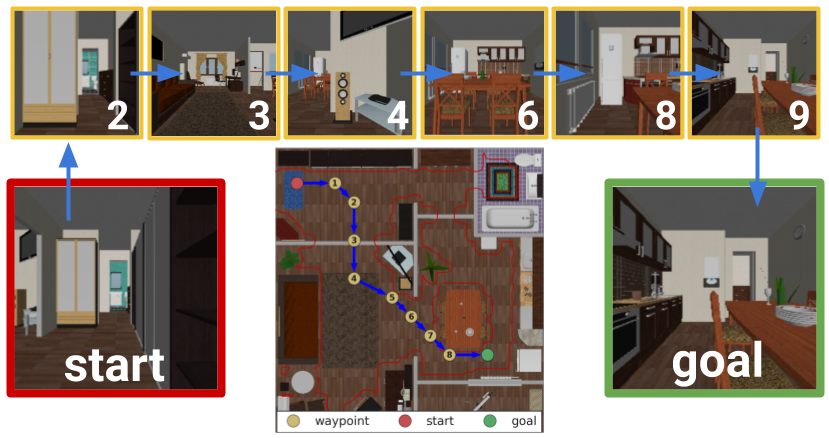 Visual Navigation: Given an initial state and goal state, our method automatically finds a sequence of intermediate waypoints. The agent then follows those waypoints to reach the goal.
Visual Navigation: Given an initial state and goal state, our method automatically finds a sequence of intermediate waypoints. The agent then follows those waypoints to reach the goal.We evaluate SoRB on high-dimensional observations on the visual navigation task illustrated to the right (based on the task in Shah 2018). The agent receives either RGB or depth images and takes actions to move North/South/East/West. The agent observes both the current image and the goal image, and should take actions that lead to the goal state. Note that it is challenging to manually construct a meaningful distance metric and goal-conditioned on pixel inputs, so it is difficult to apply standard planning algorithms to this task. We compare SoRB against four state-of-the-art prior methods: hindsight experience replay (HER), distributional RL (C51), semi-parametric topological memory (SPTM), and value iteration networks (VIN).
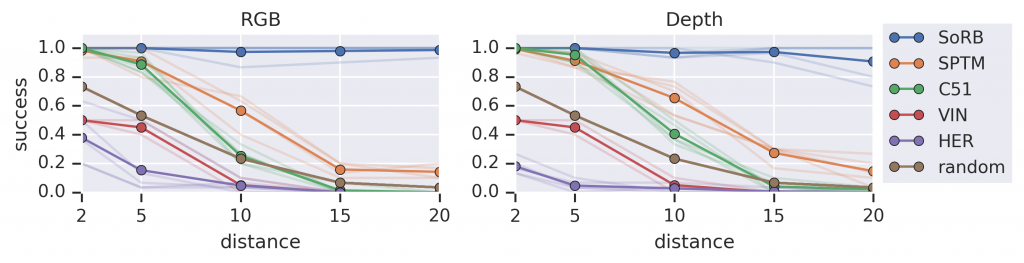 Visual Navigation: We compare our method (SoRB) to prior work on the visual navigation environment, using RGB images and depth images. We find that only our method succeeds in reaching distant goals.
Visual Navigation: We compare our method (SoRB) to prior work on the visual navigation environment, using RGB images and depth images. We find that only our method succeeds in reaching distant goals.
As shown in the plot above, all prior methods degrade quickly as the distance to the goal increases. In contrast, our method continues to succeed in reaching goals with probability around 90%. SPTM, the only prior method that also employs search, performs second best, but substantially worse than our method, likely because SPTM estimates distances using a distance metric based on one policy but uses a different policy to actually navigate between states.
 Does SoRB Generalize? After training on 100 SUNCG houses, we collect random data in held-out houses to use for search in those new environments. Whether using depth images or RGB images, SoRB generalizes well to new houses, reaching almost 80% of goals 10 steps away, while goal-conditioned RL reaches less than 20% of these goals.
Does SoRB Generalize? After training on 100 SUNCG houses, we collect random data in held-out houses to use for search in those new environments. Whether using depth images or RGB images, SoRB generalizes well to new houses, reaching almost 80% of goals 10 steps away, while goal-conditioned RL reaches less than 20% of these goals.
We now study whether our method generalizes to new visual navigation environments. We train on 100 houses, randomly sampling one per episode, and evaluated on a held-out test set of 22 houses. In each house, we collect 1000 random observations and fill our replay buffer with those observations to perform search. We use the same goal-conditioned policy and associated distance function that we learned during training. In the figure above, we observe that SoRB reaches almost 80% of goals that are 10 steps away, about four times more than reached by the goal-conditioned RL agent.
Next Steps
SoRB is just one way of combining planning and reinforcement learning, and we are excited to see future work explore other combinations. Some concrete open problems are (1) using search to improve the policy learned by goal-conditioned RL and (2) determining how this approach fairs on other simulated and real-world domains. If interested, we have released code to run SoRB in your browser, as well as a list of more open problems: http://bit.ly/rl_search.
DISCLAIMER: All opinions expressed in this post are those of the author and do not represent the views of CMU.