The Rise of Artificial Intelligence
Over the past decade, artificial intelligence (AI) has achieved remarkable success in many fields such as healthcare, automotive, and marketing. The capabilities of sophisticated, autonomous decision systems driven by AI keep evolving and moving from lab to reality. Many of these systems are black-box which means we don’t really understand how they work and why they reach such decisions.
The Dangers of Black-Box
As black-box decision systems have come into greater use, they have also come under greater criticism. One of the main concerns is that it is dangerous to rely on black-box decisions without knowing the way they are made. Here is an example of why they can be dangerous.
Risk-assessment tools have been widely used in the federal and state courts to facilitate and improve judges’ decisions in the criminal justice processes. They provide defendants’ future criminal risk based on socio-economic status, family background, and other factors. In May 2016, ProPublica claimed that one of the most widely used risk-assessment tools, COMPAS, was biased against black defendants while being more generous to white defendants [link]. Northpointe, a for-profit company that provides the software, disputed the analysis but refused to disclose the software’s decision mechanism. So it is not possible for either stakeholders or the public to see what might be actually creating the disparity.
The Need for Interpretability
It is dangerous to rely on black-box decisions without knowing the way they are made. Here, we raise a question: How can we possibly go about resolving this concern? Explaining how a black-box decision system works or why it reaches such decisions helps to decide whether or not to follow its decisions. The need for interpretability is especially urgent in fields where black-box decisions can be life-changing and have significant consequences, such as disease diagnosis, criminal justice, and self-driving cars.
What is a desired explanation?
Explanations should be brief but comprehensive.
What makes a ‘good’ explanation for a black-box? Assume that you give a black-box predictive model an image of an apple. You open the black-box and explain why it believes this is indeed an apple on the image. Simply saying that “it is red, so this is an apple” is not sufficient to justify your thought, but you should also avoid redundant explanation. It is important to give enough information concisely in explaining a black-box decision system. In other words, explanations should be brief but comprehensive.
Variational Information Bottleneck for Interpretation
How can we take into account both briefness and comprehensiveness for explaining a black-box? Our work uses an information theoretic perspective to quantify the idea of briefness and comprehensiveness.
The information bottleneck principle (Tishby et al., 2000) provides an appealing information theoretic view for learning supervised models by defining what we mean by a ‘good’ representation. The principle says that the optimal model transmits as much information as possible from its input to its output through a compressed representation called the information bottleneck. And the information bottleneck is a good representation that is maximally informative about the output while compressive about a given input. Recently, Shwartz-Ziv et al. (2017) and Tishby et al. (2015) showed that the principle also applies to deep neural networks and each layer of the networks can work as an information bottleneck.
We adopt the information bottleneck principle as a criterion for finding a ‘good’ explanation. In the information theoretic view, we define a brief but comprehensive explanation as maximally informative about the black-box decision while compressive about a given input. In other words, the explanation should maximally compress the mutual information regarding an input while preserving as much as possible mutual information regarding its output.
Variational Information Bottleneck for Interpretation
We introduce the variational information bottleneck for interpretation (VIBI), a system-agnostic information bottleneck model that provides a brief but comprehensive explanation for every single decision made by a black-box.
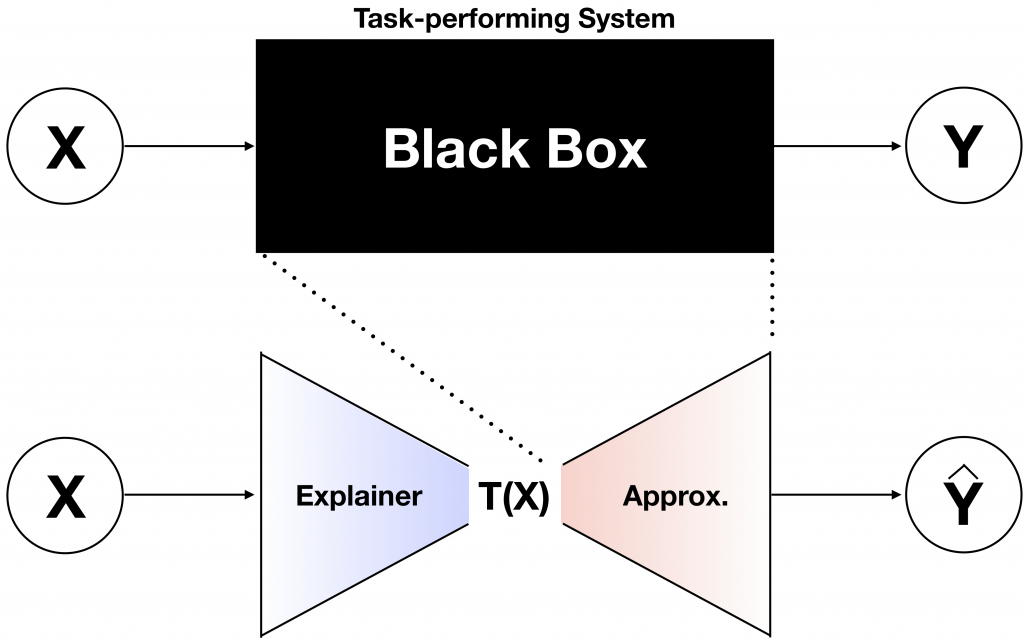Overview of VIBI. The top is a black-box decision system to be explained. The bottom is our proposed model for explaining the black-box. VIBI is composed of two parts: explainer and approximator, each of which is modeled by a deep neural network. Using the information bottleneck principle, VIBI learns an explainer that favors brief explanations while enforcing that the explanations alone suffice for an accurate approximation to the black-box. See the following illustration for an illustration of VIBI.
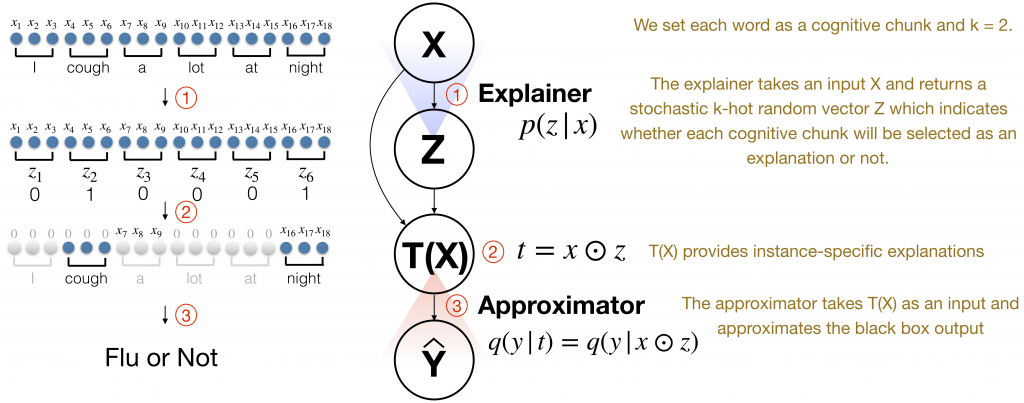
For each instance, the explainer returns a probability whether a chunk of features, called a cognitive chunk, will be selected as an explanation or not. Cognitive chunk is defined as a group of raw features that work as a unit to be explained and whose identity is recognizable to a human, such as a word, phrase, sentence or a group of pixels. The selected chunks act as an information bottleneck that is maximally compressed about input and informative about the decision made by a black-box system on that input.
Now, we formulate the following optimization problem inspired by the information bottleneck principle to learn the explainer and approximator:
$$ p(\mathbf{z} | \mathbf{x}) = \mathrm{argmax}_{p(\mathbf{z} | \mathbf{x}), p(\mathbf{y} | \mathbf{t})} ~~\mathrm{I} ( \mathbf{t}, \mathbf{y} ) – \beta~\mathrm{I} ( \mathbf{x}, \mathbf{t} )$$ where \( \mathrm{I} ( \mathbf{t}, \mathbf{y} ) \) represents the sufficiency of information retained for explaining the black-box output \( \mathbf{y} \), \(-\mathrm{I} ( \mathbf{x}, \mathbf{t} ) \) represents the briefness of the explanation \( \mathbf{t} \), and \( \beta \) is a Lagrange multiplier representing a trade-off between the two.
Challenges in Learning VIBI
The current form of information bottleneck objective is intractable due to the mutual informations and the non-differentiable sample \( \mathbf{z} \). We address these challenges as follows.
Variational Approximation to Information Bottleneck Objective
The mutual informations \( \mathrm{I} ( \mathbf{t}, \mathbf{y} ) \) and \( \mathrm{I} ( \mathbf{x}, \mathbf{t} ) \) are computationally expensive to quantify (Tishby et al., 2000; Chechik et al., 2005). In order to reduce the computational burden, we use a variational approximation to our information bottleneck objective: $$\mathrm{I} ( \mathbf{t}, \mathbf{y} )~-~\beta~\mathrm{I} ( \mathbf{x}, \mathbf{t} )
\geq \mathbb{E}_{\mathbf{y} \sim p(\mathbf{x})} \mathbb{E}_{\mathbf{y} | \mathbf{x} \sim p(\mathbf{y} | \mathbf{x})} \mathbb{E}_{\mathbf{t} | \mathbf{x} \sim p(\mathbf{t} | \mathbf{x})} \left[ \log q(\mathbf{y} | \mathbf{t}) \right] ~-~\beta~\mathbb{E}_{\mathbf{x}\sim p(\mathbf{x})} \mathrm{KL} (p(\mathbf{z}| \mathbf{x}), r(\mathbf{z})) $$
Now, we can integrate the Kullback-Leibler divergence \( \mathrm{KL} (p(\mathbf{z}| \mathbf{x}), r(\mathbf{z})) \) analytically with proper choices of \( r(\mathbf{z}) \) and \( p(\mathbf{z}|\mathbf{x}) \). We also use the empirical data distribution to approximate \( p(\mathbf{x}, \mathbf{y}) = p(\mathbf{x})p(\mathbf{y}|\mathbf{x}) \).
Continuous Relaxation and Re-parameterization
We use the generalized Gumbel-softmax trick (Jang et al., 2017; Chen et al., 2018), which approximates the non-differentiable categorical subset sampling with Gumbel-softmax samples that are differentiable. This trick allows using standard backpropagation to compute the gradients of the parameters via reparameterization.
Result
VIBI provides instance-specific keywords to explain an LSTM sentiment prediction model using Large Movie Review Dataset, IMDB.
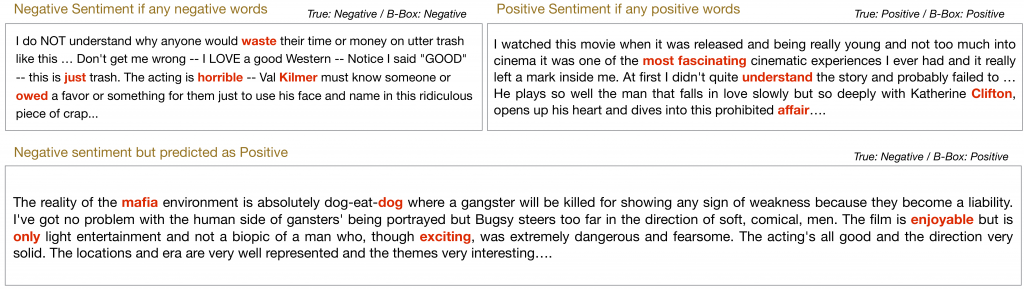Explanation for the LSTM movie sentiment prediction model using IMDB. The selected words (k = 5) are colored red.
The keywords such as “waste,” and “horrible,” are selected for the negative-predicted movie review, while keywords such as “most fascinating,” explain the model’s positive-predicted movie review. Also, we could see that the LSTM sentiment prediction model makes a wrong prediction for a negative review because the review includes several positive words such as ‘enjoyable’ and ‘exciting’.
VIBI also provides instance-specific key patches containing \( 4 \times 4 \) pixels to explain a CNN digit recognition model using the MNIST image dataset.
Explanation for the CNN digit recognition model using MNIST. The selected patches (k = 4) are colored red if the pixel is activated (i.e. white) and yellow otherwise (i.e. black).
The first two examples show that the CNN recognizes digits using both shapes and angles. In the first example, the CNN characterizes ‘1’s by straightly aligned patches along with the activated regions although ‘1’s in the left and right panels are written at different angles. Contrary to the first example, the second example shows that the CNN recognizes the difference between ‘9’ and ‘6’ by their differences in angles. The last two examples show that the CNN catches a difference of ‘7’s from ‘1’s by patches located on the activated horizontal line on ‘7’ (see the cyan circle) and recognizes ‘8’s by two patches on the top of the digits and another two patches at the bottom circle.
VIBI Explains Black-box Models Better
We assume that a better explanation allows humans to better infer the black-box output given the explanation. Therefore, we asked humans to infer the output of the black-box system (Positive/Negative/Neutral) given five keywords as an explanation generated by VIBI and other competing methods (Saliency, LIME, and L2X). Each method was evaluated by the human intelligences on Amazon Mechanical Turk who are awarded the Masters Qualification (i.e. high-performance workers who have demonstrated excellence across a wide range of tasks). We also evaluated the interpretability for the CNN digit recognition model using MNIST. We asked humans to directly score the explanation on a 0 to 5 scale (0 for no explanation, 1-4 for insufficient or redundant explanation and 5 for concise explanation). Each method was evaluated by 16 graduate students at the School of Computer Science, Carnegie Mellon University who have taken at least one graduate-level machine learning class.
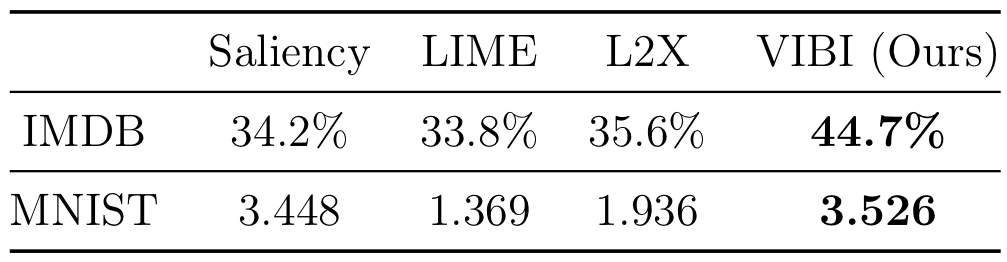For IMDB, the percentage indicates how well the MTurk worker’s answers match the black box output. For MNIST, the score indicates how well the highlighted chunks catch key characteristics of the handwritten digits. The average scores over all samples are shown on a 0 to 5 scale.VIBI Approximates Black-box Models Better
We assessed fidelity of the approximator by prediction performance with respect to the black- box output. We introduce two types of formalized metrics to quantitatively evaluate the fidelity: approximator fidelity and rationale fidelity.
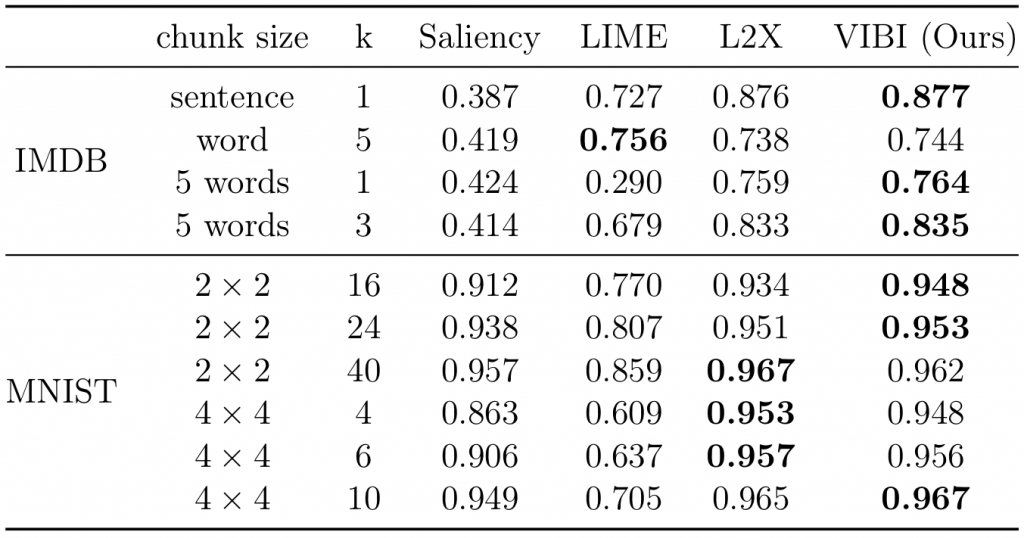Evaluation of approximator fidelity. Accuracy is shown.Approximator fidelity implies the ability of the approximator to imitate the behaviour of a black-box. As shown above, VIBI and L2X outperform the others in approximating the black-box models. However, it does not mean both approximators are same in fidelity. See below.
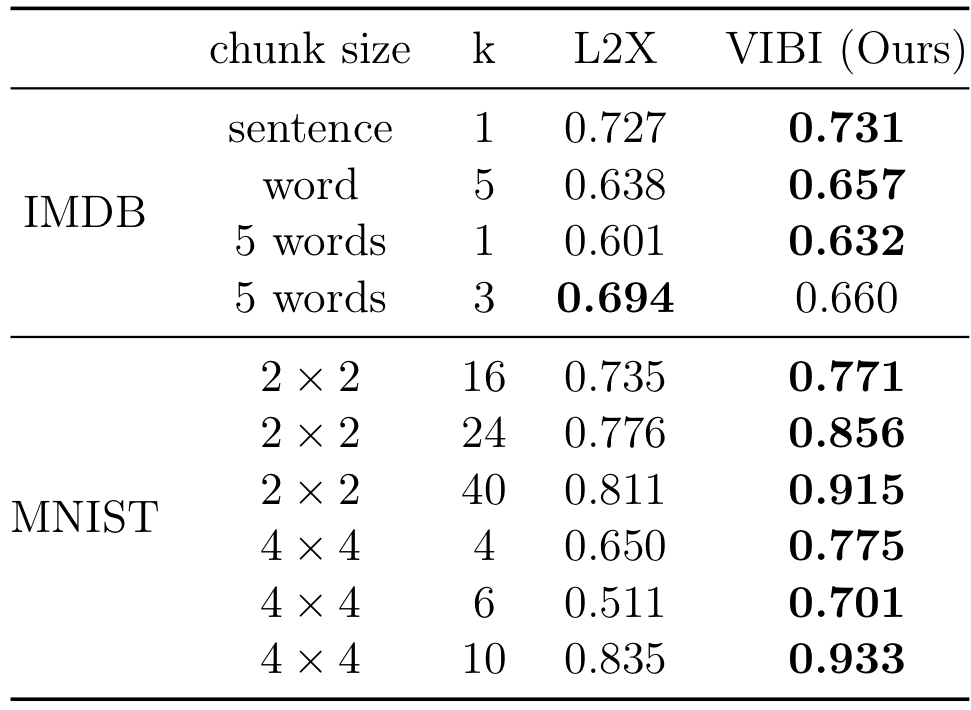Evaluation of rationale fidelity. Rationale fidelity implies how much the selected chunks contribute to the approximator fidelity. As shown above, the selected chunks of VIBI account for more approximator fidelity than L2X. Note that L2X is a special case of VIBI having the information bottleneck trade-off parameter \( \beta = 0 \) (i.e. not using the compressiveness constraint \( −\mathrm{I} ( \mathbf{x}, \mathbf{t} ) \)). Therefore, compressing information through the explainer achieves not only conciseness of explanation but also better fidelity of explanation to a black-box.
Note that the number of cognitive chunks to be selected, \( k \), should be given in advance. It also impacts conciseness of the actual total explanation and should be chosen carefully. In our analysis, we choose \( k \) as the minimum number that exceeds a certain fidelity.
Where Should I Look to Learn More?
Further details can be found here. The code is publicly available here.
DISCLAIMER: All opinions expressed in this post are those of the author and do not represent the views of CMU.
